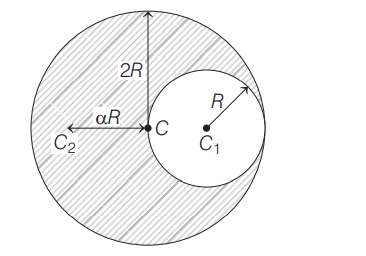
Question

A circular disc of radius $R$ is removed from one end of a bigger circular disc of radius $2 \,R$. The centre of mass of the new disc is at a distance $\alpha R$ from the centre of the bigger disc. The value of $\alpha$ is

• A. $\frac{1}{2}$
• B. $\frac{1}{3}$
• C. $\frac{1}{4}$
• D. $\frac{1}{6}$

Answer 1

Answer: (B)

Let, mass of entire disc $=M$
Mass per unit area $=\frac{M}{\pi(2 R)^{2}}=\frac{M}{4 \pi R^{2}}$
Mass of removed disc of radius $R$
$M_{1}=\frac{M}{4 \pi R^{2}} \times R^{2}=\frac{ M }{4}$
Mass of remaining disc,
$\Rightarrow M_{2}=M-\frac{M}{4}=\frac{3 M}{4}$
Center of mass of removed disc is $C_{1}$ and centre of
mass of remaining new disc is $C_{2}$.
And centre of mass of combination of $M_{1}$ and $M_{2}$ will be at $C(0,0)$.
$\Rightarrow \frac{M_{1} x_{1}-M_{2} x_{2}}{M_{1}-M_{2}}=0$
$\Rightarrow M_{1} \,x_{1}=M_{2}\, x_{2} $
$\frac{M}{4} \cdot R=\frac{3 M}{4}(\alpha R) $
$\Rightarrow \alpha=\frac{1}{3}$