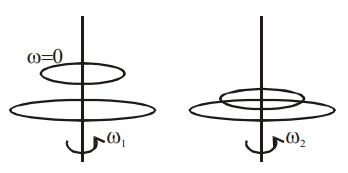
Question

A circular disc of mass $M$ and radius $R$ is rotating about its axis with angular speed $\omega_{1}$. If another stationary disc having radius $\frac{ R }{2}$ and same mass $M$ is dropped co-axially on to the rotating disc. Gradually both discs attain constant angular speed $\omega_{2}$. The energy lost in the process is $p\%$ of the initial energy. Value of $p$ is ______.

Answer 1

Let moment of inertia of bigger disc is $I=\frac{M R^{2}}{2}$
$\Rightarrow $ MOI of small disc $I_{2}=\frac{M\left(\frac{R}{2}\right)^{2}}{2}=\frac{I}{4}$
by angular momentum conservation
$I \omega_{1}+\frac{ I }{4}(0)= I \omega_{2}+\frac{ I }{4} \omega_{2} $
$\Rightarrow \omega_{2}=\frac{4 \omega_{1}}{5}$
initial kinetic energy $K _{1}=\frac{1}{2} I \omega_{1}^{2}$
final kinetic energy $K _{2}$
$=\frac{1}{2}\left( I +\frac{ I }{4}\right)\left(\frac{4 \omega_{1}}{5}\right)^{2}=\frac{1}{2} I \omega_{1}^{2}\left(\frac{4}{5}\right) $
$P \%= \frac{ K _{1}- K _{2}}{ K _{1}} \times 100 \%$
$=\frac{1-4 / 5}{1} \times 100=20 \%$