Q. A circular current carrying coil has a radius R The distance from the centre of the coil off the axis of the coil, where the magnetic induction is I/8th of its value at the centre of the coil is
ManipalManipal 2008Moving Charges and Magnetism
Solution:
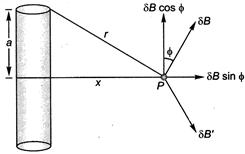
For a circular coil of radius a carrying a current $ i $ , the magnetic field at point $ P $ , distance $ x $ from coil is given by
$ B=\frac{{{\mu }_{0}}i\,\,{{a}^{2}}}{2{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}N{{A}^{-1}}{{m}^{-1}} $ .. (i)
At the centre of coil $ x=0 $
$ \therefore $ $ B=\frac{{{\mu }_{0}}i}{2a}N{{A}^{-1}}{{m}^{-1}} $ .. (ii)
Given, $ B=\frac{1}{8}B $
$ \therefore $ $ \frac{{{\mu }_{0}}i\,\,{{a}^{2}}}{2{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}=\frac{1}{8}\left( \frac{{{\mu }_{0}}i}{2a} \right) $
$ \Rightarrow $ $ \frac{{{a}^{2}}}{{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}=\frac{1}{8a} $
$ \Rightarrow $ $ 8\,\,{{a}^{3}}={{({{a}^{2}}+{{x}^{2}})}^{3/2}} $
$ \Rightarrow $ $ {{a}^{2}}+{{x}^{2}}=4{{a}^{2}} $
$ \Rightarrow $ $ x=\sqrt{3\cdot a} $
Given, $ a=R $ $ x=\sqrt{3}\,\,R $