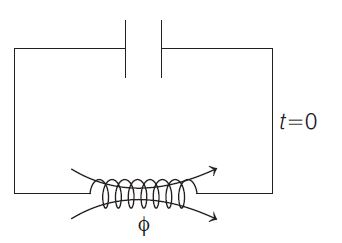
Question

A circuit consists of a coil with inductance $L$ and an uncharged capacitor of capacitance $C$. The coil is in a constant uniform magnetic field such that the flux through the coil is $\phi$. At time $t=0 min$, the magnetic field is abruptly switched OFF. Let $\omega_{0}=1 / \sqrt{L C}$ and ignore the resistance of the circuit. Then,

• A. current in the circuit is $I (t) =(\phi/L)\cos\omega_0t$
• B. magnitude of the charge on the capacitor is $|Q(t)|= 2C\omega_0|\sin\omega_0t|$
• C. initial current in the circuit is infinite
• D. initial charge on the capacitor is $C\omega_0\phi$

Answer 1

Answer: (A)

At $t = 0$ capacitor is uncharged and flux of inductor is $\phi.$

Now, using $\phi = LI,$ at $t = 0$ current in circuit is
$I_{0}=\frac{\phi}{L}$
Instantaneous current in circuit is $\frac{dq}{dt}.$
where, $q$ is solution of
$L\frac{d^{2}\,q}{dt^{2}}+\frac{q}{C}=o$
or $\frac{d^{2}\,q}{dt^{2}}+\frac{q}{LC}=o$
At $t = 0,$ current in circuit is non-zero,
so instantaneous current is given by
$=I_{0} \cos \omega t =\frac{\phi}{L} . \cos\omega t$