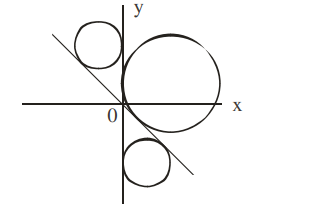1. Tardigrade
  2. Question
  3. Mathematics
  4. A circle touches both the y-axis and the line x+y=0. Then the locus of its center is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. A circle touches both the $y$-axis and the line $x+y=0$. Then the locus of its center is

JEE MainJEE Main 2022Conic Sections

Solution:

Let $(h, k)$ is centre of circle
$\left|\frac{ h - k }{\sqrt{2}}\right|=| h |$
$ k ^{2}- h ^{2}+2 hk =0$
$\therefore$ Equation of locus is $y ^{2}- x ^{2}+2 xy =0$

Solution Image