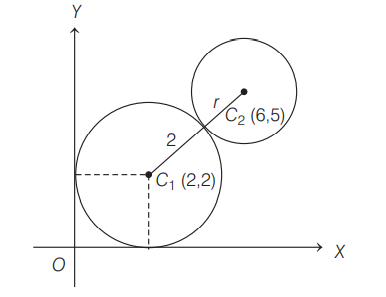
Question

A circle $S$ of radius $2$ units lies in the first quadrant and touches both the coordinate axes. The equation of the circle with centre at $(6,5)$ and touching the circle $S$ externally is

• A. $x^{2}+y^{2}-12 x-10 y+12=0$
• B. $x^{2}+y^{2}-12 x-10 y-20=0$
• C. $x^{2}+y^{2}-12 x-10 y+25=0$
• D. $x^{2}+y^{2}-12 x-10 y+52=0$

Answer 1

Answer: (D)

From figure

Centre of given circle $\left(C_{1}\right)=(2,2)$ radius $=2$ units
Centre of required circle $\left(C_{2}\right)=(6,5)$
$C_{1} C_{2} =r+2$
$5 =r+2$
$\therefore \, r =3$
$\therefore $ Required equation of circle having centre at $(6,5)$ and $r=3$ is
$(x-6)^{2}+(y-5)^{2}=3^{2} $
$x^{2}+y^{2}-12 x-10 y+52=0$