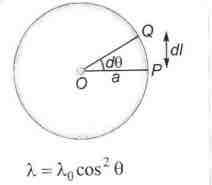
Q. A circle of radius a has charge density given by $ \lambda = \lambda_0 \, \cos^2 \, \theta$ on its circumference. What will be the total charge on the circle?
Gujarat CETGujarat CET 2008Electric Charges and Fields
Solution:
Charge density Let PQ be an element of length dl on the circumference of the circle which makes an angle $d \theta$ at the centre of the circle.
Then the charge on the element is
$dq = \lambda \times dl$
$\Rightarrow dq = \lambda_0 \, \cos^2 \, \theta dl$ ..(i)
Now, $ d \theta = \frac{ dl}{ a} \Rightarrow dl = ad \, \theta $
Then from Eq. (i)
d$q = \lambda_0 \, \cos^2 \, \theta . ad \, \theta $
$\Rightarrow dq = \lambda_0 a\cos^2 \theta d \theta$ ...(ii)
The total charge on the circle [ on integrating Eq. (ii) with limit 0 to 2 $\pi$]
$q = \int \limits_0^{ 2 \pi} \lambda_0 a \, \cos^2\, \theta d \, \theta$
or $q = \lambda_0 a \int \limits_0^{ 2 \pi} \frac{ \cos \, 2 \theta + 1}{ 2} d \theta $
$\left [ \because \cos^2 \, \theta = \frac{ \cos \, 2 \theta + 1}{ 2}\right] $
$\Rightarrow q = \frac{ \lambda_0 a }{ 2} \left[ \frac{ \sin \, 2 \theta }{ 2} + \theta \right] _0^{ 2 \pi} $
$\Rightarrow q = \frac{ \lambda_0 a }{ 2} \left[ \frac{ \sin \, 4 \pi}{ 2} + 2 \pi - \frac{ \sin \, 0 }{ 2} - 0\right] $
$\Rightarrow q = \frac{ \lambda_0 a }{ 2} [ 0 + 2\pi - 0 ] $
$\Rightarrow q = \pi a \lambda_0$