Question

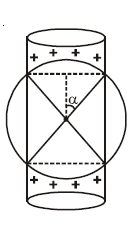
A charged shell of radius $R$ carries a total charge $Q$. Given $\Phi$ as the flux of electric field through a closed cylindrical surface of height $h$, radius $r$ and with its center same as that of the shell. Here, center of the cylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Which of the following option(s) is/are correct?
[$\varepsilon_{0}$ is the permittivity of free space]

• A. If $h > 2R$ and $r > R$ then $\pi=Q/\in_{0}$
• B. If $h < 8R/5$ and $r = 3R/5$ then $\pi = 0$
• C. If $h > 2R$ and $r = 3R/5$ then $\pi=Q/5\in_{0}$
• D. If $h > 2R$ and $r = 4R/5$ then $\pi=Q/5\in_{0}$

Answer 1

Answer: (A), (B), (C)

For option (A) : $\left(h>2R\,r=\frac{3R}{5}\right)$
$sin\,\alpha=\frac{r}{R}=\frac{3}{5}$
$cos\,\alpha=\frac{4}{5}$
$Q_{enclosed}=\frac{Q}{5}$
$\therefore \phi=\frac{Q}{5\,\in_{0}}$
For option (B) : $h<\frac{8R}{5}, r=\frac{3R}{5}$
$Q_{enclosed}=0$
and $\phi=0$
For option (C) : ($h > 2R$ and $r > R$)
$Q_{enclosed} = Q$
$\therefore \phi=\frac{Q}{\in_{0}}$
For option (D) : $h>2R\,r=\frac{4R}{5}$
$Q_{enclosed}=Q\left[1-cos\,\alpha\right]$
$sin\,\alpha=\frac{r}{R}=\frac{3}{5}$
and $cos\,\alpha=\frac{3}{5}\,Q_{enclosed}=\frac{2Q}{5}$
$\therefore \phi=\frac{2Q}{5\in_{0}}$