Q.
A charged particle $q$ is placed at the centre $O$ of cube of length $L$ $(ABCDEFGH)$. Another same charge $q$ is placed at a distance $L$ from $O$. Then the electric flux through $ABCD$ is :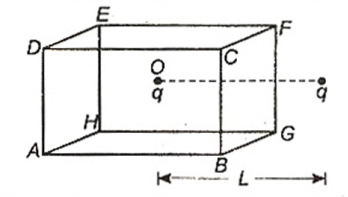
AIEEEAIEEE 2002Electric Charges and Fields
Solution:
