Question

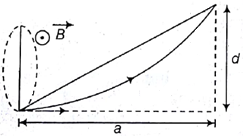
A charged particle $q$ enters a region of uniform magnetic field $B$ (out of page) and is deflected distance $d$ after travelling a horizontal distance a. The magnitude of the momentum of the particle is

• A. $\frac{q B}{2}\left[\frac{a^{2}}{d} + d\right]$
• B. $\frac{q B}{2}$
• C. Zero
• D. $2qB$

Answer 1

Answer: (A)

From the figure given below we have, $AB=\sqrt{a^{2} + d^{2}}=h$
$AB=\sqrt{a^{2} + d^{2}}=h$
In $\Delta OAD, \, cos\theta =\frac{h}{2 R}$
In $\Delta ACB,sin\left(\frac{\pi }{2} - \theta \right)=\frac{d}{h}$
$\Rightarrow \frac{h}{2 R}=\frac{d}{h}$
$\Rightarrow h^{2}=2Rd$
$\Rightarrow a^{2}+d^{2}=2Rd$

$\Rightarrow R=\frac{a^{2}}{2 d}+\frac{d}{2}$
$\therefore $ Momentum, $P=mv$
$=qBR=\frac{q B}{2}\left(\frac{a^{2}}{d} + d\right)\left[\because R = \frac{m v}{q B}\right]$