Q.
A charged particle of mass $'m'$ and charge $'q'$ moving under the influence of uniform electric field $E\overrightarrow{i}$ and a uniform magnetic field $B\overrightarrow{k}$ follows a trajectory from point $P$ to $Q$ as shown in figure. The velocities at $P$ and $Q$ are respectively, $v\overrightarrow{i}$ and $-2v\overrightarrow{i}.$ Then which of the following statements (A, B, C D) are the correct ? (Trajectory shown is schematic and not to scale)
$\left(A\right)\quad E = \frac{3}{4}\left(\frac{m\upsilon^{2}}{qa}\right)$
$\left(B\right) \quad$ Rate of work done by the electric field at $P$ is $\frac{3}{4} \left(\frac{m\upsilon^{3}}{a}\right)$
$\left(C\right) \quad$ Rate of work done by both the fields at $Q$ is zero
$\left(D\right) \quad$ The difference between the magnitude of angular momentum of the particle at $P$ and $Q$ is $2\, ma \upsilon.$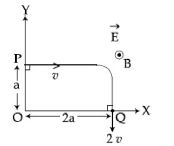
Solution: