Q.
A charged particle having charge $10^{-6} C$ and mass of $10^{-10} kg$ is fired the middle of the plate making an angle $30^{\circ}$ with plane of the plate. Length of the plate is $0.17\, m$ and it is separated by $0.1\, m$. Electric field $E=10^{-3} N / C$ is present between the plates. Just outside the plates magnetic field is present. Find the magnitude of the magnetic field (in $mT$ ) of the charged particle perpendicular to the plane of the figure, if it has to graze the plate at $C$ and $A$ parallel to the surface of the plate (neglect gravity).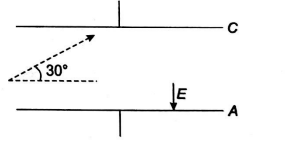
Moving Charges and Magnetism
Solution: