Q.
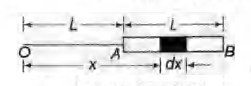
A charge $Q$ is uniformly distributed over a long rod $AB$ of length $L$ as shown in the figure. The electric potential at the point $O$ lying at distance $L$ from the end A is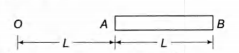
Solution:
$V=\int\limits_{L}^{2 L} \frac{k d Q}{x}=\int\limits_{L}^{2 L} \frac{k\left(\frac{Q}{L}\right) d x}{x}=\frac{Q}{4 \pi \varepsilon_{0} L} \int\limits_{L}^{2 L}\left(\frac{1}{x}\right) d x$
$=\frac{Q}{4 \pi \varepsilon_{0} L}\left[\log _{e} x\right]_{L}^{2 L}$
$=\frac{Q}{4 \pi \varepsilon_{0} L}\left[\log _{e} 2 L-\log _{e} L\right]=\frac{Q}{4 \pi \varepsilon_{0} L} In(2)$