1. Tardigrade
  2. Question
  3. Physics
  4. A charge q is uniformly distributed on a ring of radius r. A sphere of an equal radius is constructed with its centre lying on the periphery of the ring. The flux of electric field through the surface of the sphere will be

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

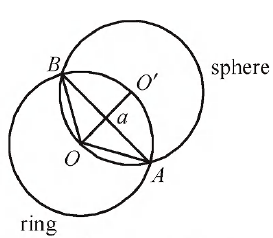
Q. A charge $q$ is uniformly distributed on a ring of radius $r$. A sphere of an equal radius is constructed with its centre lying on the periphery of the ring. The flux of electric field through the surface of the sphere will be

AIIMSAIIMS 2008Electric Charges and Fields

Solution:

Charge on ring $q$, centre of ring $=O$
Centre of sphere $=O'$
Linear charge density of ring, $\lambda=\frac{q}{2 \pi a}$ Charge on arc $A B$ of ring,
$q_{A B}=\lambda(\operatorname{arc} A B)=\frac{1}{2 \pi a} \cdot a \cdot \frac{2 \pi}{3}$
$q_{A B}=q / 3$
i.e.., charged enclosed by sphere $=q / 3$
$\therefore $ Flux coming out of sphere $=q / 3 \varepsilon_{0}$

Solution Image