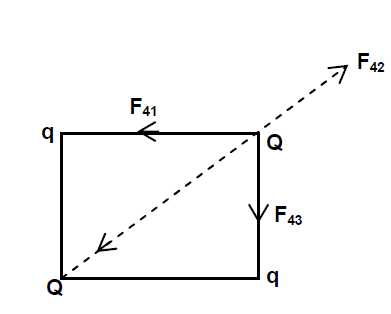
Q. A charge $Q$ is placed at each of the opposite corners of a square. A charge $q$ is placed at each of the other two corners. If the net electrical force on $Q$ is zero, then the $Q/q $ equals
AIEEEAIEEE 2009Electric Charges and Fields
Solution:
Three forces $F_{41}, F_{42}$ and $f_{43}$ acting on $Q$ are shown Resultant of $F_{41} + F_{43}$
$=\sqrt{2}\,F_{each}$
$=\sqrt{2} \frac{1}{4\pi\varepsilon_{o}} \frac{Qq}{d^{2}}$
Resultant on Q becomes zero only when ‘q’ charges are of negative nature.
$F_{4, 2}= \frac{1}{4\pi\varepsilon_{o}} \frac{Q\times Q}{\left(\sqrt{2}d\right)^{2}}$
$\Rightarrow \sqrt{2} \frac{dQ}{d^{2}}=\frac{Q\times Q}{2}$
$\Rightarrow \sqrt{2}\times q=\frac{Q\times Q}{2}$
$\therefore q=-\frac{Q}{2\sqrt{2}}$ or $\frac{Q}{q}=-2\sqrt{2}$