Question

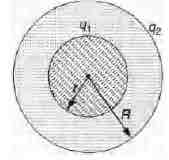
A charge Q is distributed over two concentric hollow spheres
of radii r and $ R (> r)$ such that the surface densities are equal.
Find the potential at the common centre.

Answer 1

Let $q_1$ and $q_2$ be the charges on them.
$\sigma_1 - \sigma_2$
$\therefore \frac{q_1}{4 \pi r^2}=\frac{q_2}{4 \pi R^2}$
$\therefore \frac{q_1}{q_2}=\frac{r^2}{R^2}$
i.e. charge on them is distributed in above ratio.
or $\, \, \, q_1=\frac{r^2}{r^2+R^2}Q \, \, $ and $\, \, \, q_2=\frac{R^2}{r^2+R^2}Q $
Potential at centre V = potential due to $q_1$ + potential due to $q_2$
or $ V=\frac{1}{4 \pi\varepsilon_0}.\frac{q_1}{r}+\frac{1}{4 \pi\varepsilon_0}.\frac{q_2}{R}$
$ =\frac{Q(R+r)}{4 \pi\varepsilon_0 (r^2+R^2)}$