Q.
A charge $Q$ is distributed over two concentric conducting thin spherical shells radii $r$ and $R$ $( R > r )$. If the surface charge densities on the two shells are equal, the electric potential at the common centre is :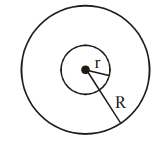
Solution:
