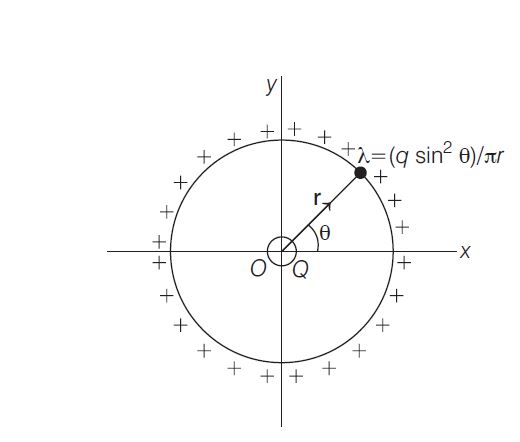
Question

A charge $+q$ is distributed over a thin ring of radius $r$ with line charge density $\lambda = q\,\sin^{2} \theta/(\pi r)$. Note that the ring is in the $XY-$ plane and $\theta$ is the angle made by r with the $X-$axis. The work done by the electric force in displacing a point charge $+ Q$ from the centre of the ring to infinity is

• A. equal to $qQ / 2\, \pi \varepsilon _o r$
• B. equal to $qQ / 4 \,\pi \varepsilon _o r$
• C. equal to zero only, if the path is a straight line perpendicular to the plane of the ring
• D. equal to $qQ / 8\,\pi \varepsilon _o r$

Answer 1

Answer: (B)

As charge distribution is over a circle, potential due to charge over ring is
$V=\frac{k}{r} \cdot q_{\text{total}}$
where, $q_{\text {total }}=\int\limits_{0}^{2 \pi} \frac{q \sin ^{2} \theta}{\pi r}(r d \theta)$
$=\frac{q}{\pi} \int\limits_{0}^{2 \pi} \frac{1-\cos 2 \theta}{2} \cdot d \theta $
$=\frac{q}{\pi}\left[\left(\frac{\theta}{2}-\frac{\sin 2 \theta}{4}\right)\right]_{0}^{2 \pi}=q$
So, potential at centre of ring $=V$
$=\frac{k q_{\text {total }}}{r} $
$\Rightarrow V =\frac{k q}{r}$
Also, work done in taking a charge $Q$ from centre of ring to infinity $=$ potential energy of system
$=V \cdot Q=\frac{k q Q}{r}=\frac{q Q}{4 \pi \varepsilon_{0} r}$