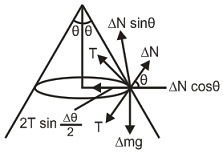
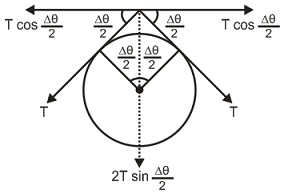
Question

A chain of mass $m$ forming a circle of radius $R$ is slipped on a smooth round cone with half-angle $\theta$ . Find the tension in the chain if it rotates with a constant angular velocity $\omega $ about a vertical axis coinciding with the symmetry axis of the cone.

• A. $\left(R \omega^2+g \cot \theta\right) \frac{m}{2 \pi}$
• B. $\left(R \omega^2-\mathrm{g} \cot \theta\right) \frac{m}{2 \pi}$
• C. $\left(R \omega^2+\mathrm{g} \cot \theta\right) \frac{m}{\pi}$
• D. $(R \omega-\mathrm{g} \cot \theta) \frac{m}{2 \pi}$

Answer 1

Answer: (A)

Every element of chain moves on a circular path. So, every element of the chain experiences centripetal force. We consider a small element $\Delta \text{m}$ on the chain making angle $\Delta \theta $ at the centre


$\Delta N \sin \theta=\Delta mg$ ...... (i)
Net force towards centre is
$2 \text{T} \text{sin} \frac{\Delta \theta }{2} - \Delta \text{N} \text{cos} \theta = \Delta \text{mR} \omega ^{2}$
$\Delta N \text{cos} \theta = 2 T ⁡ \text{sin} \frac{\Delta \theta }{2} - \Delta \text{mR} \omega ^{2}$ .......... (ii)
From eqn.(i) and (ii) we get
$\text{cos} \theta = \frac{2 \text{T} \text{sin} \frac{\Delta \theta }{2} - \Delta \text{mR} \omega ^{2}}{\Delta \text{mg}}$
But $Δ \theta $ is very small.
∴ $\text{sin} \frac{\Delta \theta }{2} = \frac{\Delta \theta }{2}$
∵ $\text{cot} \theta = \frac{\text{T} \Delta \theta - \Delta \text{mR} \omega ^{2}}{\Delta \text{mg}}$
Here Δm makes an angle Δθ at the centre. The total mass of chain is m.
∴ The mass of chain per unit angle is
$\lambda = \frac{m }{2 \pi }$
∴ $\Delta m = \lambda \Delta \theta = \frac{m ⁡}{2 \pi } \Delta \theta = \frac{m ⁡ \Delta \theta }{2 \pi }$
∴ $\text{cot} \, \, \theta = \frac{\text{T} \Delta \theta - \left(\frac{m \Delta \theta }{2 \pi }\right) R \left(\omega \right)^{2}}{\left(\frac{m}{2 \pi } \Delta \theta \right) g}$
$\therefore T=\left(R \omega^{2}+ g \cot \theta\right) \frac{m}{2 \pi}$