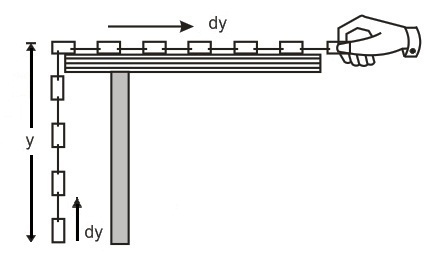
Question

A chain is held on a frictionless table with $1/n$ th of its length hanging over the edge. If the chain has a length $L$ and a mass $M$ , how much work is required to pull the hanging part back on the table?

• A. $\frac{M g L^{}}{2 n^{2}}$
• B. $\frac{M g L}{n^{2}}$
• C. $\frac{M g L}{4 n^{3}}$
• D. $\frac{M g L}{3 n^{- 1}}$

Answer 1

Answer: (A)

If $m$ is the mass per unit length of the chain, the mass of the chain of length $y$ will be $y\times m=ym$ and the force acting on it due to gravity will be $my\times g=mgy$ (assuming that $y$ is the length of the chain hanging over the edge). So, the work done in pulling the $dy$ length of the chain on the table
$dW=F\left(- d y\right)$ [as $y$ is decreasing]
i.e., $dW=mgy\left(\right.-dy\left.\right)$ [as $F=mgy$ ]
So, the work done in pulling the hanging portion on the table :
$W =-\int\limits_{ L / n }^0 mgydy =\frac{ MgL ^2}{2 n ^2}$
orW $= MgL / 2 n ^2[$ as $M = mL ]$