Question

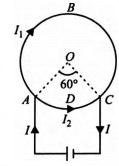
A cell is connected between the points A and C of a circular conductor $ABCDA$ of centre $O \angle AOC=60^{\circ} $ If $B_{1}$ and $B_{2}$ are the magnitudes of the magnetic fields at $O$ due to currents in $ABC$ and $ADC$ respectively, the ratio $B_{1} / B_{2}$, is

• A. 6
• B. 5
• C. 1
• D. 1/5

Answer 1

Answer: (C)

Let $l_{1}, l_{2}$ be the lengths of the two parts $ABC$ and $ADC$ of the conductor and $\rho$ be resistance per unit length of the conductor.
The resistance of the part $ABC$ will be
$R_{1}=\rho l_{1} / A$
The resistance of the part $ADC$ will be
$R_{2}=\rho\, l_{2} / A$
Potential difference across $AC$ must be equal $=I_{1} R_{1}=I_{2} R_{2}$
or $I_{1} \rho l_{1} / A=I_{2} \rho l_{2} / A$ or $ I_{1} l_{1}=I_{2} l_{2} \,\,\,\,\dots(i)$
Magnetic field at $O$ due to a current $I_{1}$ flowing in $A B C$ is given by
$B_{1}=\frac{\mu_{0} I_{1} \theta_{1}}{4 \pi r}=\frac{\mu_{0} I_{1} l_{1}}{4 \pi r^{2}}$ (As $l_{1}=\theta_{1} r)$
Magnetic field at $O$ due to current $I_{2}$ flowing in $ADC$ is given by
$B_{2}=\frac{\mu_{0} I_{2} \theta_{2}}{4 \pi r}=\frac{\mu_{0}}{4 \pi} \frac{I_{2} l_{2}}{r^{2}} $
(As $l_{2}=\theta_{2} r)$
$\therefore \frac{B_{1}}{B_{2}}=1$ [Using (i)]