Question

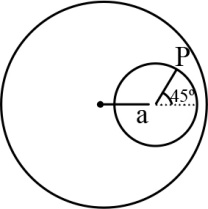
A cavity of radius $r$ is made inside a solid sphere. The volume charge density of the remaining sphere is $\rho $ . An electron (charge $e$ , mass $m$ ) is released from rest inside the cavity from point $P$ as shown in the figure. The centre of the sphere and centre of the cavity are separated by a distance $a$ . The time after which the electron again touches the sphere is

• A. $\sqrt{\frac{6 \sqrt{2} r \epsilon _{0} m}{e \rho a}}$
• B. $\sqrt{\frac{\sqrt{2 r} \epsilon _{0} m}{6 \rho a}}$
• C. $\sqrt{\frac{6 r \epsilon _{0} m}{e \rho a}}$
• D. $\sqrt{\frac{r \epsilon _{0} m}{e \rho a}}$

Answer 1

Answer: (A)

$E \, = \, \frac{\rho a}{3 \epsilon _{0}} \, F \, = \, eE \, = \, \frac{e \rho a}{3 \epsilon _{0}}$
acceleration $= \, \frac{\rho e a}{3 m \epsilon _{0}}$



$= \, \frac{1}{2}\times \frac{\rho e a}{3 m \epsilon _{0}}\times t^{2} \, = \, \sqrt{2}r$
$\Rightarrow t=\sqrt{\frac{6 \sqrt{2} r \epsilon _{0} m}{e \rho a}}$ The electron will move opposite to electronic field with constant acceleration along shown horizontal line of length $= \sqrt{2} r$