Q.
A Cassegrain telescope uses two mirrors as shown in figure. Such a telescope is built with the mirrors $20\, mm$ apart. If the radius of curvature of the large mirror is $220 \,mm$ and the small mirror is $140\, mm$, where will the final image of an object at infinity be?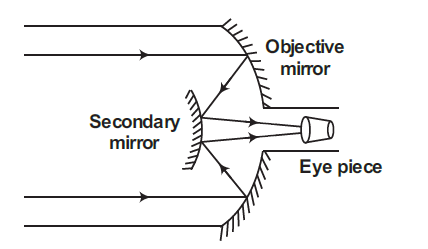
Ray Optics and Optical Instruments
Solution: