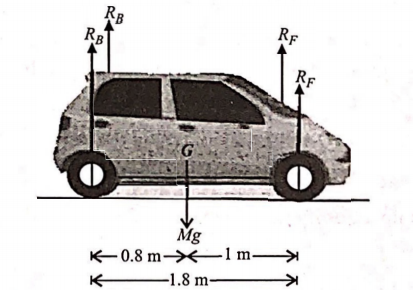
Question

A car weighs $1800 \,kg$. The distance between its front and back axles is $1.8 \,m$. Its centre of gravity is $1 \,m$ behind the front axle. The force exerted by the level ground on each front wheel and each back wheel is (Take $g = 10\, m s^{-2})$

• A. $4000 \,N$ on each front wheel, $5000 \,N$ on each back wheel
• B. $5000\, N$ on each front wheel, $4000 \,N$ an each back wheel
• C. $4500\, N$ on each front wheel, $4500 \,N$ on each back wheel
• D. $3000 \,N$ on each front wheel, $6000 \,N$ on each back wheel

Answer 1

Answer: (A)

Here, mass of the car, $M = 1800\, kg$
Distance between front and back axles $= 1.8\, m$
Distance of gravity G behind the front axle $= 1 \,m$
Let $R_F$ and $R_B$ be the forces exerted by the level ground on each front wheel and each back wheel.

For translational equilibrium,
$2 R_F + 2 R_B = Mg$
or $R_F +R_B = \frac{Mg}{2} = \frac{1800 \times 10}{2} $
$ = 9000\,N\quad ...(i)$
(As there are two front wheels and two back wheels) For rotational equilibrium about $G$
$(2R_F )(1) = (2R_B)(0.8)$
$\frac{R_F}{R_B} = 0.8 $
$ = \frac{8}{10} = \frac {4}{5}$
$\Rightarrow R_F = \frac{4}{5}R_B \quad ...(ii)$
Substituting this in Eq.$ (i)$, we get
$\frac{4}{5} R_B = 9000$ or $ \frac{9}{5}R_B = 9000$
$R_B = \frac{9000\times 5}{9} = 5000\,N$
$\therefore R_F = \frac{4}{5}R_B $
$= \frac{4}{5}\times 5000\,N$
$ = 4000\,N$