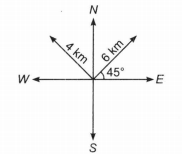
Q. A car travels 6 km towards north at an angle of 45$^{\circ}$ to the east and then travels distance of 4 km towards north at an angle 135$^{\circ}$ to east. How far is the point from the starting point? What angle does the straight line joining its initial and final positions makes with the cast?
Motion in a Plane
Solution:
Net movement along X-direction
$ S_x = (6 - 4) cos 45^\circ \hat i$
$ = 2 \times \frac{1}{\sqrt2} = \sqrt2 \, km$
Net movement along Y -direction
$ S_y = (6 + 4) sin 45^\circ \hat j$
$ = 10 \times \frac{1}{\sqrt2} = 5 \sqrt2 \, km$
Net movement from starting point
$ |S| = \sqrt{S_x^2 + S_y^2} = \sqrt{(\sqrt2)^2 + (5 \sqrt2)^2}$
$ = \sqrt{52} \, km$
Angle which resultant makes with the east direction
$ tan \, \theta = \frac{y - component}{x - component}$
$ = \frac{5 \sqrt2}{\sqrt2}$
$\therefore 40mm \theta = \tan^{-1} (5)$