Q.
A car moves with speed $v$ on a horizontal circular track of radius $R$. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is $h$, and the separation between its inner and outer wheels is $d$. The road is dry, and the car does not skid. The maximum speed the car can have without overturning is.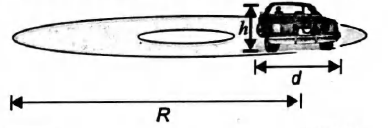
System of Particles and Rotational Motion
Solution:
