Q.
A car driver is trying to jump across a path as shown in figure by driving horizontally off a cliff ' $X$ ' at the speed 10 $m / s$. When he touches peak $Z$ (ignore air resistance), what would be speed?
$\text { (use } g=10 \,m / s ^2 \text { ) }$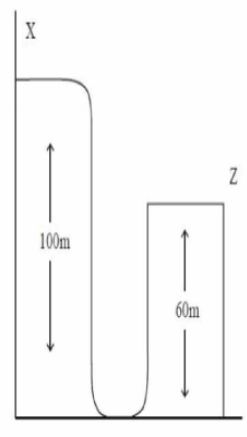
TS EAMCET 2021
Solution:
