Q.
A capacitor of capacitance $3\, \mu F$ is first charged by connecting it across a $10\, V$ battery by closing key $K_{1}$, then it is allowed to get discharged through $2\, \Omega$ and $4 \, \Omega$ resistors by opening $K_{1}$ and closing the key $K_{2}$. The total energy dissipated in the $2\, \Omega$ resistor is equal to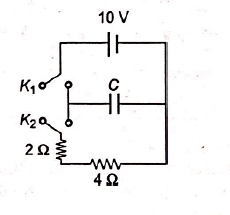
Current Electricity
Solution: