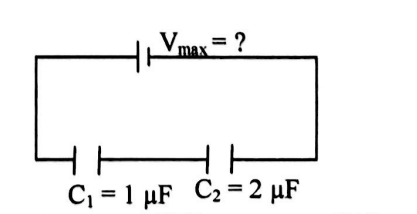
Question

A capacitor of capacitance $1\, \mu F$ withstands a maximum voltage of $6\, kV$, while another capacitor of capacitance $2\, \mu F$, the maximum voltage $4 \, kV$. If they are connected in series, the combination can withstand a maximum of - (in $kV )$

Answer 1

$V_{1 \max }=6\, KV $
$V_{2 \max }=4 \,KV$
$q=C V$
$V \propto \frac{1}{C}$
If we proceed according to $V _{\max }$ of $2$
$V _{1}: V _{2} =2: 1 $
$\Rightarrow V _{2 \max } =\frac{1}{3} V _{\max }$
$ V _{1} =\frac{2}{3} \times V \,\,\,4=\frac{1}{3} V _{\max } $
$ V _{1_{\max }} =\frac{2}{3} V _{\max } \,\,\,V _{\max }=12 KV $
$ 6 =\frac{2}{3} V _{\max } \,\,\,V _{1}=\frac{2}{3} \times V _{\max } $
$ V _{\max } =9\, KV =\frac{2}{3} \times 12 $
$ V _{2} =\frac{1}{3} V _{\max }=8 \,KV $
$ V _{2} =3 \,KV$
Which exceeds $V_{1}$ max limit Valid
$\therefore $ Not valid