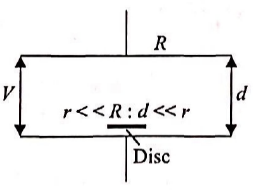
Question

A capacitor is made of two circular plates of radius $R$ each, separated by a distance $d <\,<\, R$. The capacitor is connected to a constant voltage. A thin conducting disc of radius $r<\,<\, R$ and thickness $t <\,<\, r$ is placed at the centre of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is $m$.

• A. $\frac{\sqrt{mgd}}{\pi\varepsilon_{0} r^{2}}$
• B. $\sqrt{\frac{mgd}{\pi\varepsilon_{0}r}}$
• C. $\sqrt{\frac{mgd^{2}}{\pi\varepsilon_{0}r^{2}}}$
• D. $\sqrt{\frac{mgd}{\pi\varepsilon_{0}r^{2}}}$

Answer 1

Answer: (C)

As shown in figure, the disc is in touch with the bottom plate. The electric field on the disc is $E=V/d$ Therefore, charge $q'$ transferred to the disc
$q'=CV=\left(\frac{\varepsilon_{0} A}{d}\right) V=\varepsilon_{0} \frac{V}{d} \pi r^{2}$
Force acting on the disc, $F=q' E=\left(\varepsilon_{0}\frac{V}{d}\pi r^{2}\right) \frac{V}{d}$
$F=\varepsilon_{0} \frac{V^{2}}{d^{2}} \pi r^{2}$
If the disc is to be lifted, $F \ge\, mg$,
i.e., $\varepsilon_{0} \frac{V^{2}}{d^{2}} \pi r^{2}=mg$
(for minimum $V$)
$\therefore V=\sqrt{\frac{mgd^{2}}{\pi\varepsilon_{0}r^{2}}}$