Question

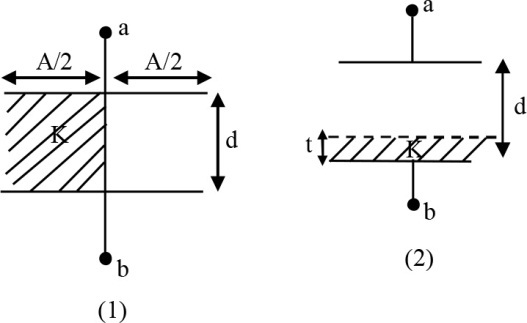
A capacitor is half filled with a material of dielectric $\left(K = 2\right)$ as shown in diagram (1). If the same material is to be filled in the same capacitor as shown in diagram (2), then find the thickness of dielectric in 2nd case so that capacitance of capacitor remains same in both case ?

• A. $\frac{2 d}{3}$
• B. $\frac{3 d}{2}$
• C. $\frac{3 d}{4}$
• D. $\frac{4 d}{3}$

Answer 1

Answer: (A)

$C′=\frac{\in _{0} A}{2 d} \, C"=\frac{C_{0} K}{2}$
$\therefore C_{1}=C′+C′′$
$\therefore C_{1}=\frac{C_{0}}{2}+\frac{C_{0} K}{2}=\frac{C_{0}}{2} \, \left(1 + K\right)$
(Equivalent capacitance of $1^{s t}$ diagram)




$C_{2}=\frac{\in _{0} A}{d \, - \, t + \frac{t}{K}}$
(Equivalent capacitance of $2^{n d}$ diagram)
Both are same hence :
$\frac{C_{0}}{2} \, \left(K + 1\right)=\frac{\left(\in \right)_{0} A}{d \, - \, t + \frac{t}{K}}$
$\frac{\left(\in \right)_{0} A}{2 d} \, \left(2 + 1\right)=\frac{\left(\in \right)_{0} A}{d \, - \, t + \frac{t}{2}}$
$3d \, - \, \frac{3 t}{2}=2d$
$d=\frac{3 t}{2} \, or \, t=\frac{2 d}{3}$