Q.
A capacitor having capacitance $1 \,\mu F$ with air, is filled with two dielectric as shown. How many times capacitance will increase?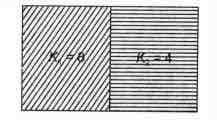
Delhi UMET/DPMTDelhi UMET/DPMT 2006Electrostatic Potential and Capacitance
Solution:
As shown, the two capacitors are connected in parallel.
Initially the capacitance of capacitor
$C=\frac{\varepsilon_{0} A}{d}$
where $A$ is area of each plate and dis the separation between the plates.
After filling with dielectrics,
we have two capacitors of capacitance
$C_{1}=\frac{K_{1} \varepsilon_{0}(A / 2)}{d}$
$=\frac{8}{2} \frac{\varepsilon_{0} A}{d}=\frac{4 \varepsilon_{0} A}{d}=4 c$
and $C_{2}=\frac{{ }^{d} \frac{K_{2} \varepsilon_{0}(A / 2)}{d}}{d_{0}}$
$\frac{4}{2} \frac{\varepsilon_{0} A}{d} = \frac{2 \varepsilon_{0} A}{d}=2 C$
Hence, their equivalent capacitance
$C=C_{1}+C_{2} $
$=4 C+2 C $
$=6 C$
ie, new capacitance will be six time of the original.