Q.
A capacitor $C_1=1.0 \, \mu \, F$ is charged up to a voltage $V\, =\, 60 \,V$ by connecting it to battery $B$ through switch $(1)$. Now $C_1$ is disconnected from battery and connected to a circuit consisting of two uncharged capacitors $C_2 = 3.0 \, \mu F$ and $C_3 = 6.0 \, \mu F$ through switch $(2)$, as shown in the figure. The sum of final charges on $C_2$ and $C_3$ is :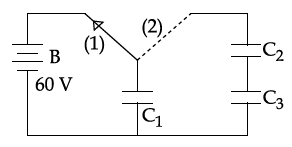
Solution:
