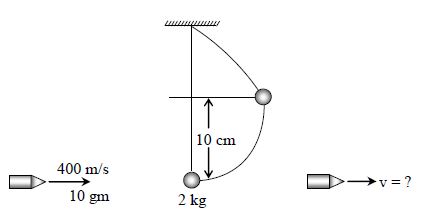
Q. A bullet of mass $10\,g$ moving horizontally with a velocity of $400 \, ms^{-1}$ strikes a wooden block of mass $2 \,kg$ which is suspended by a light inextensible string of length $5\, m$. As a result, the centre of gravity of the block is found to rise a vertical distance of $10\,cm$. The speed of the bullet after it emerges out horizontally from the block will be -
Solution:
Velocity of block = $\sqrt{2gh} = \sqrt{2 \times g \times 0.1} = \sqrt{2} \, m/s$
$P_i = P_f$
$(10 \times 10^{-3} ) \times 400 + 0 = 2 \times \sqrt{2} + (10 \times 10^{-3} ) V$
$V = \frac{(4 - 2 \sqrt{2})}{10 \times 10^{-3}} = 120 \, m/s$