1. Tardigrade
  2. Question
  3. Physics
  4. A bullet of mass 0.02 kg travelling horizontally with velocity 250 ms-1 strikes a block of wood of mass 0.23 kg which rests on a rough horizontal surface. After the impact, the block and bullet move together arid come to rest after travelling a distance of 40 m. The coefficient of sliding friction of the rough surface is ( g = 9.8 ms-2)

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

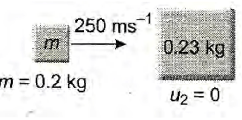
Q. A bullet of mass $0.02 \,kg$ travelling horizontally with velocity $250\, ms^{-1}$ strikes a block of wood of mass $0.23 \,kg$ which rests on a rough horizontal surface. After the impact, the block and bullet move together arid come to rest after travelling a distance of $40 \,m$. The coefficient of sliding friction of the rough surface is $( g = 9.8 \, ms^{-2}) $

BITSATBITSAT 2009

Solution:

After impact the bullet and block move together and come's to rest after covering a distance of $40 \,m$.
By conservation of momentum ,
$m_1 u_1 + m_2u_2 = m_1 v_1+ m_2v_2$
or $0.02 \times 250 + 0.23 \times 0 = 0.02 \, v + 0.23 \, v $
$5 + 0 = v (0.25) $
$ \frac{500}{25} v = 20 \, ms^{-1}$
Now, by conservation of energy
$ \frac{1}{2} Mv^2 = \mu R . d$
or $ \frac{1}{2} \times 0.25 \times 400 = \mu \times 0.25 \times 9.8 \times 40$
$\Rightarrow \, \mu = \frac{200}{ 9.8 \times 40} = 0.51 $

Solution Image