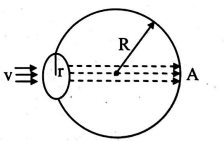
Question

A bubble having surface tension $T$ and radius $R$ is formed on ring of radius $r ( r << R )$. Air of density $\rho$ is blown inside the tube with velocity $v$ such that air molecule collides perpendicularly with the wall of the bubble and stops. The radius at which the bubble separates from the ring is $\frac{Z T}{\rho v^{2}}$. Find $Z$.

Answer 1

Excess pressure inside a bubble $=\frac{4 T}{R}$
Let area of wall of bubble where air strikes be $A$.

$\therefore $ Force due to excess pressure $=\frac{4 TA }{ R }$
Now, force due to striking air $=\rho Av ^{2}$ For bubble to separate from the ring,
$\rho A v^{2}=\frac{4 T A}{R}$
$\Rightarrow R=\frac{4 T}{\rho v^{2}}$
$\Rightarrow Z=4$