1. Tardigrade
  2. Question
  3. Physics
  4. A boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle of 30° with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground? (g=10 m/s2, sin 30o=1/2, cos 30o=√3/2)

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

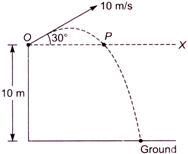
Q. A boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle of $ 30{}^\circ $ with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground? $ (g=10\,m/{{s}^{2}},\,\sin {{30}^{o}}=1/2,\,\cos {{30}^{o}}=\sqrt{3}/2) $

Rajasthan PMTRajasthan PMT 2008Motion in a Plane

Solution:

The ball will be at point $ P $ when it is at a height of $ 10\,\,m $ from the ground. So, we have to find distance $ OP $ , which can be calculated direct considering it as a projectile on a levelled $ (OX) $ .
$ OP=R=\frac{{{u}^{2}}\sin 2\theta }{g} $ $ =\frac{{{10}^{2}}\times \sin (2\times {{30}^{o}})}{10} $ $ =\frac{10\sqrt{3}}{2}=5\sqrt{3} $ $ =8.66\,\,m $

Solution Image