Q.
A bottle has an opening of radius $a$ and length $b$. A cork of length $b$ and radius $(a+ \Delta a)$ where $(\Delta a < < a)$ is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is $B$ and frictional coefficient between the bottle and cork is $\mu$ then the force needed to push the cork into the bottle is :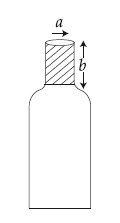
Solution: