Q. A body takes time $t$ to reach the bottom of an inclined plane of angle $ \theta $ with the horizontal. If the plane is made rough, time taken now is $2t$. The coefficient of friction of the rough surface is:
Delhi UMET/DPMTDelhi UMET/DPMT 2005Laws of Motion
Solution:
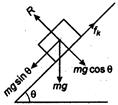
The free body diagram shows the various forces acting on the block. When plane is frictionless, then acceleration, $a=g \sin \theta$.
Let time taken is $t_{1}$ Since body starts from rest, initial velocity $u=0$
$\therefore s=u t+\frac{1}{2} a t_{1}^{2}$
$\Rightarrow s=\frac{1}{2} g \sin \theta t_{1}^{2}$
$\Rightarrow t_{1}=\sqrt{\frac{2 s}{g \sin \theta}}$
When plane is made rough, then acceleration $a = g (\sin \theta-\mu \cos \theta)$, where $\mu$ is coefficient of friction.
$\therefore t_{2}=\sqrt{\frac{2 s}{g(\sin \theta-\mu \cos \theta)}}$
Given, $t_{2}=2 t_{1}$
$\therefore \sqrt{\frac{2 s}{g(\sin \theta-\mu \cos \theta)}}$
$=2 \sqrt{\frac{2 s}{g \sin \theta}}$
$\therefore \frac{1}{\sin \theta-\mu \cos \theta}=\frac{4}{\sin \theta}$
$\Rightarrow \sin \theta=4 \sin \theta-4 \mu \cos \theta$
$\Rightarrow \mu=\frac{3}{4} \tan \theta$