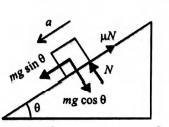
Question

A body placed on the surface of a smooth inclined plane reaches the bottom of the plane in time $t$. When it is identically placed on a rough inclined plane, it reaches the bottom in time $n t$ where $n>1$. In both the cases, the angle of inclination $\theta$ is same. The coefficient of friction $\mu$ is equal to

• A. $\sin \theta\left[1-\frac{1}{n^{2}}\right]$
• B. $\cos \theta\left[1-\frac{1}{n^{2}}\right]$
• C. $\tan \theta\left[1-\frac{1}{n^{2}}\right]$
• D. $\tan \theta$

Answer 1

Answer: (C)

$m g \sin \theta=m a$ or $a=g \sin \theta$
$s=\frac{1}{2}(g \sin \theta) t^{2} ; t=\left(\frac{2 s}{g \sin \theta}\right)^{\frac{1}{2}}$

$N=m g \cos \theta ; m g \sin \theta-\mu m g \cos \theta=m a$
$\Rightarrow a=g \sin \theta-\mu g \cos \theta$
$s=\frac{1}{2}(g(\sin \theta-\mu \cos \theta))(n t)^{2} \Rightarrow n t=\left[\frac{2 s}{g(\sin \theta-\mu \cos \theta)}\right]$
$\Rightarrow n\left(\frac{2 s}{g \sin \theta}\right)^{\frac{1}{2}}=\left(\frac{2 s}{g(\sin \theta-\mu \cos \theta)}\right)^{\frac{1}{2}}$
$\Rightarrow \frac{n^{2}}{\sin \theta}=\frac{1}{\sin \theta-\mu \cos \theta}$
$n^{2} \sin \theta-\mu n^{2} \cos \theta=\sin \theta$
$\left(n^{2}-1\right) \sin \theta=\mu n^{2} \cos \theta$
$\mu=\left(\frac{n^{2}-1}{n^{2}}\right) \cdot \tan \theta \Rightarrow \mu=\left(1-\frac{1}{n^{2}}\right) \cdot \tan \theta$