Q. A body of mass m slides down on a rough plane inclination a. If $ \mu $ is the coefficient of friction, the acceleration of the body will be
ManipalManipal 2013Laws of Motion
Solution:
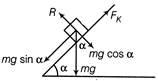
When a body descends, the frictional free acts upwards. The free body diagram given situation is as shown in the figure.
When the body is moving down, frictional force acts upwards. Now the body descends under the action of the force mg. since
$ -{{F}_{k}} $ .
If downward acceleration is a, then,
$ mg\sin \alpha -{{F}_{k}}=ma $
Where $ {{F}_{k}}=\mu R=\mu mg\cos \alpha $
$ \therefore $ $ mg\sin \alpha -\mu mg\cos \alpha =ma $
$ \Rightarrow $ $ a=g(\sin \alpha -\mu \cos \alpha ) $