Q. A body of mass $M$ at rest explodes into three pieces, two of them of mass $M/4$ each, are thrown off in perpendicular directions with velocities of $3\, m/s$ and $4 \,m/s$ respectively. The third piece will be thrown off with a velocity of
Delhi UMET/DPMTDelhi UMET/DPMT 2010
Solution:
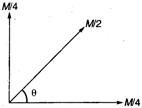
Let one mass piece of mass $M / 4$ be thrown off in the horizontal direction with a speed of $3\, m / s$, and the other mass piece of mass $M / 4$ be thrown in the vertical direction with a speed of $4 \, m / s$ and the remaining mass $M / 2$ be thrown with a velocity $v\, m/s$, making an angle $\theta$ with the horizontal direction.
So, from conservation of momentum,
Along horizontal direction
$\frac{M}{4} \times 3+\frac{M}{2} \times v \cos \theta=0 \ldots$ (i)
Along vertical direction
$\frac{M}{4} \times 4+\frac{M}{2} \times v \sin \theta=0 \ldots$ (ii)
So, from Eqs. (i) and (ii), we get
$v \cos \theta=-\frac{3}{2} \ldots$ (iii)
and $v \sin \theta=-2 \ldots$ (iv)
So, $v=\sqrt{(3 / 2)^{2}+(2)^{2}}$
$=\sqrt{9 / 4+4}=\frac{5}{2}$