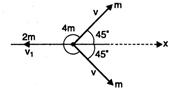
Q. A body of mass 4m at rest explodes into three pieces. Two of the pieces each of mass m move with a speed v each in mutually perpendicular directions. The total kinetic energy released is:
VMMC MedicalVMMC Medical 2003
Solution:
Total mass = 4m Two pieces, each has mass $ =\text{ }m $ Third piece has a mass $ =4m-m-n $
By law of conservation of momentum $ 2m{{\upsilon }_{1}}=m\upsilon \cos {{45}^{o}}+m\upsilon \cos {{45}^{o}} $ $ =\frac{m\upsilon }{\sqrt{2}}+\frac{m\upsilon }{\sqrt{2}}=\frac{2m\upsilon }{\sqrt{2}} $ $ \therefore $ $ {{\upsilon }_{1}}=\frac{\upsilon }{\sqrt{2}} $ Therefore, K.E. $ =\frac{1}{2}m{{\upsilon }^{2}}+\frac{1}{2}m{{\upsilon }^{2}}+\frac{1}{2}2m\upsilon _{1}^{2} $ $ m{{\upsilon }^{2}}+m{{\left( \frac{\upsilon }{\sqrt{2}} \right)}^{2}}=m{{\upsilon }^{2}}+\frac{m{{\upsilon }^{2}}}{2}=\frac{3}{2}m{{\upsilon }^{2}} $