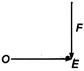
Q. A body of mass $2\, kg$ has an initial velocity of $5\, ms ^{-1}$ along $O E$ and it is subjected to a force of $4 N$ in a direction perpendicular to $O E$. The distance of the body from $O$ after $4 s$ will be
AMUAMU 2003
Solution:
From Newton's law
$F = ma$
where $m$ is mass and $a$ the acceleration.
Given, $F=4 \,N , m=2 \,kg$
$\therefore a=\frac{F}{m}=\frac{4}{2}=2 \,ms ^{-2}$
Also, distance covered by body is
$d=4 \times 5=20\, m$
From equation of motion, displacement $(y)$ is given by
$y=u t+\frac{1}{2} a t^{2}$
Given, $u=0 ; a=2 \,ms ^{-2}, t=4 s$
$\therefore y=0+\frac{1}{2} \times 2 \times(4)^{2}=16\, m$
In vector form, displacement is given by
$s=x \hat{ i }+y \hat{ j } $
$s=20 \hat{ i }+16 \hat{ j }$
Hence, distance from $O$ is
$|s| =\sqrt{20^{2}+16^{2}} $
$|s| =\sqrt{400+256} $
$|s| =25.6 \,m $
$\Rightarrow s \approx 26\, m$