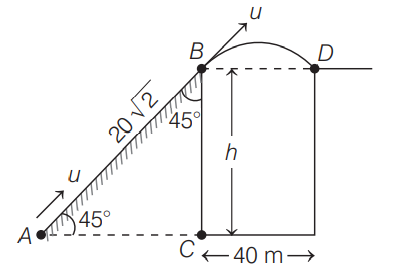
Question

A body is projected up a smooth inclined plane of length $20 \sqrt{2} \,m$ from point $A$ as shown in the figure. The top $B$ of the inclined plane is connected to a well of diameter $40 \,m$. If the body just manages to cross the well then the velocity of projection is
(Acceleration due to gravity, $g=10\, ms ^{-2}$ )

• A. $40 \, ms ^{-1}$
• B. $40 \sqrt{2} \, ms ^{-1}$
• C. $20\, ms ^{-1}$
• D. $20 \sqrt{2}\, ms ^{-1}$

Answer 1

Answer: (D)

According to the question,

In $\Delta A B C$,
$ \frac{h}{20 \sqrt{2}}=\cos 45^{\circ} $
$\Rightarrow h=20 \sqrt{2}\left(\frac{1}{\sqrt{2}}\right)$ or $ h=20\, m $
From third equation of the motion,
$ v^{2} =u^{2}+2 g h $
$\Rightarrow v =\sqrt{2 g h}\,\,\, (\because u=0) $
$\Rightarrow v =\sqrt{2 \times 10 \times 20}=20\,m / s $
Net energy at a point $B$,
$\Rightarrow \frac{1}{2} m v^{2}+m g h =\frac{1}{2} m(20)^{2}+m \times 10 \times 20 $
$=m(200+200)=400\, m $
Net energy at point $D$ to cross the well,
$E_{D}=\frac{1}{2} m v_{D}^{2}$
So, $\frac{1}{2} m v_{D}^{2}=400\, m $
$\Rightarrow v_{D}=20 \sqrt{2} \,ms ^{-1}$