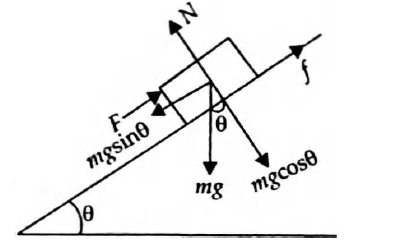
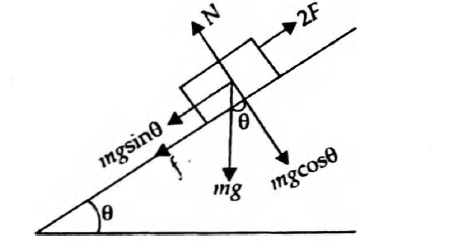
Question

A body is placed on rough $\left(\mu=\frac{1}{3\sqrt{3}}\right)$ inclined plane. $A$ force $F$ is needed to stop this body to slide downward. $A$ force $2F$ is needed so that the body is just about to move upwards. Slope of inclined plane is

• A. $30^{\circ}$
• B. $45^{\circ}$
• C. $60^{\circ}$
• D. $20^{\circ}$

Answer 1

Answer: (A)

Let $\theta$ be angle of inclination and $m$ be the mass of a body
For motion down the plane.

The equation of motion is
$F + f - mgsin \theta=0$
$F+\mu N-mgsin \theta=0$
$F+\mu mgcos\theta-mgsin\theta=0 \ldots\left(i\right)$
For motion up the plane

The equation of motion is
$2F-f-mgsin\theta=0$
$2F-\mu N-mgsin\theta=0$
$2F-\mu mgcos\theta-mgsin\theta=0 \ldots\left(ii\right)$
Adding $\left(i\right)$ and $\left(ii\right)$, we get
$3F=2mgsin\theta \ldots\left(iii\right)$
Subtracting $\left(i\right)$ from $\left(ii\right)$, we get
$F=2\mu mgcos\theta \ldots\left(iv\right)$
Dividing $\left(iii\right)$ by $\left(iv\right)$, we get
$\frac{3F}{F}=\frac{2\,mg\,sin\,\theta}{2\mu\,mg \,cos\,\theta}$
or $ tan\theta=3\mu$
$=3\times\frac{1}{3\sqrt{3}}=\frac{1}{\sqrt{3}}$
$\therefore \, \theta=30^{\circ}$