Question

A body cools in a surrounding which is at a constant temperature of $\theta_0$.

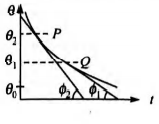
Assume that it obeys Newton’s law of cooling. Its temperature $\theta$ is plotted against time $t$ Tangents are drawn to the curve at the points $P(\theta = \theta_1)$ and $Q(\theta = \theta_2)$ These tangents meet the time axis at angles of $\phi_2$ and $\phi_1$, as shown

• A. $\frac{tan \phi_{2}}{tan \phi_{1}} = \frac{\theta_{1} - \theta_{0}}{\theta_{2}-\theta_{0}} $
• B. $\frac{tan \phi_{2}}{tan \phi_{1}} = \frac{\theta_{2} - \theta_{0}}{\theta_{1}-\theta_{0}} $
• C. $\frac{tan \phi_{1}} {tan \phi_{2}} = \frac{\theta_{1}}{\theta_{2}}$
• D. $\frac{tan \phi_{1}}{tan \phi_{2}} = \frac{\theta_{2}}{\theta_{1}}$

Answer 1

Answer: (B)

For $\theta -t$ plot, rate of cooling $= \frac{d\theta}{dt} = $slope of the curve.
At $P, \frac{d\theta}{dt} = tan\,\phi_2 = k(\theta_2 - \theta_0)$, where $k = $ constant.
At $Q \frac{d\theta}{dt} = tan\,\phi_1 = k(\theta_1 - \theta_0)$
$\Rightarrow \frac{tan\,\phi_2}{tan\,\phi_1} = \frac{\theta_2 - \theta_0}{\theta_1 - \theta_0}$