Q.
A body cools in a surrounding which is at a constant temperature of $\theta_{0}$. Assume that it obeys Newton's law of
cooling. Its temperature $\theta$ is plotted against time $t$. Tangents are drawn to the curve at the points $P\left(\theta=\theta_{1}\right)$ and $Q\left(\theta=\theta_{2}\right)$. These tangents meet the time axis at angles of $\phi_{2}$ and $\phi_{1}$, as shown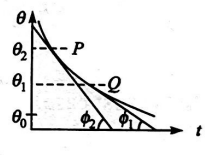
Thermal Properties of Matter
Solution: