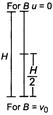
Q. A body $A$ is thrown up vertically from the ground with a velocity $v_{0}$ and another body $B$ is simultaneously dropped from a height $H$. They meet at a height $\frac{H}{2}$ if $v_{0}$ is equal to
AMUAMU 2010Motion in a Straight Line
Solution:
Suppose the two bodies $A$ and $B$ meet at time $t$,
at a height $\frac{H}{2}$ from the ground.
For body $B,\, u=0,\, h=\frac{H}{2}$
$h=u t+\frac{1}{2} g t^{2}$
$\frac{H}{2}=\frac{1}{2} g t^{2}$ ...(i)
For body $A,\, d=v_{0},\, h=\frac{H}{2}$
$h =u t-\frac{1}{2} g t^{2}$
$\frac{H}{2} =v_{0} t-\frac{1}{2} g t^{2}$ ...(ii)
From Eqs. (i) and (ii)
$v_{0} t-\frac{1}{2} g t^{2}=\frac{1}{2} g t^{2}$
or $v_{0} t=g t^{2}$
or $t=\frac{v_{0}}{g}$
Substituting the value of $t$ in Eq. (i), we get
$\frac{H}{2} =\frac{1}{2} g t^{2}$
$H =g \times\left(\frac{v_{0}}{g}\right)^{2}$
$v_{0} =\sqrt{g H}$