Question

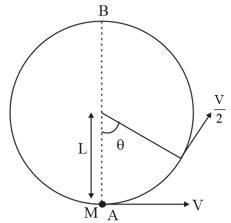
A bob of mass $\text{M}$ is suspended by a massless string of length $\text{L}$ . The horizontal velocity $\text{v}$ at position $\text{A}$ is just sufficient to make it reach point $\text{B}$ . The angle $\theta $ at which the speed of the bob is half of that at $\text{A}$ satisfies

• A. $\theta = \frac{\pi }{4}$
• B. $\frac{\pi }{4} < \theta < \frac{\pi }{2}$
• C. $\frac{\pi }{2} < \theta < \frac{3 \pi }{4}$
• D. $\frac{3 \pi }{4} < \theta < \pi $

Answer 1

Answer: (D)

Suppose at point P velocity becomes half. We also know minimum velocity required to complete the circle is
$v_{A}=\sqrt{5 g L}$
Using conservation of energy from point $A$ to $P$
$\frac{1}{2}mv_{A}^{2}=\frac{1}{2}mv_{P}^{2}+mgh$
$\frac{1}{2}mv^{2}=\frac{1}{2}m\left(\frac{v_{}}{2}\right)^{2}+mgh$
$\frac{3}{8}mv^{2}=mgh$
$\frac{3}{8}\times 5gL=ghh=\frac{15}{8}L$
$cos\left(\theta \right)=\frac{L - h}{L}=1-\frac{h}{L}=-\frac{7}{8}$
Thus option d is right answer.